El nom de les notes

Segons la Viquipèdia, “el so és una successió de canvis de pressió (compressions i dilatacions) en un medi (sòlid, líquid o gas), provocats per una vibració que s’hi transmet en forma d’ones sonores”. Aquest medi, en el nostre cas, sol ser l’aire. I les ones les podem imaginar com les que causa una pedreta que cau a l’aigua quieta d’un bassal. En una gràfica que mostrés l’alçada de cada onada, podríem representar l’ona així ¹:

![Frequencia simple

500](../img/Frequencia%20simple.jpg)

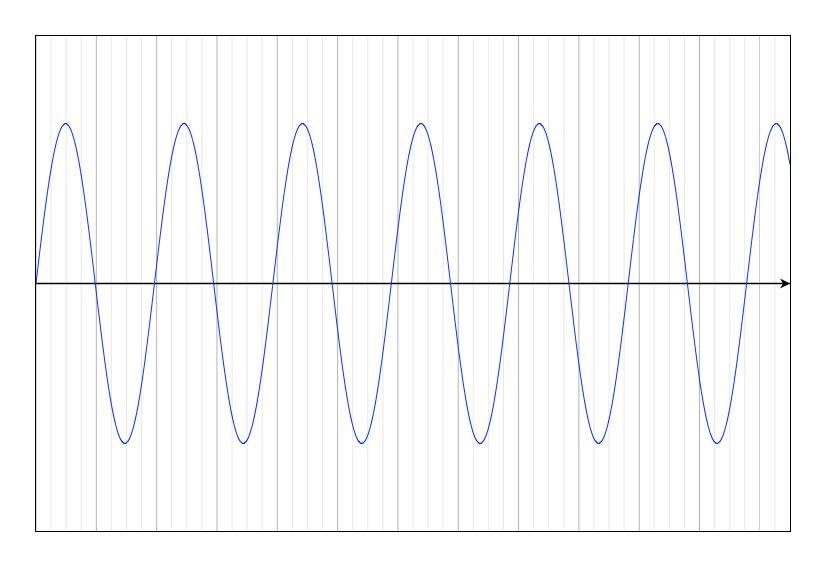Quan els físics estudien una ona com aquesta, en medeixen diverses coses. Una d’elles és la freqüència, que ens diu quantes vegades puja i baixa l’ona en un segon. La nostra oïda, tot i que varia segons la persona, típicament pot sentir aquells sons que tenen ones que es repeteixen entre 20 i 20.000 vegades per segon o, el que és el mateix, entre 20 Hz i 20.000 Hz ². Dins aquest rang, la nostra oïda percep les diferents freqüències de forma diferent: com més vegades per segon vibra l’aire, més agut sentim el so.

Però les persones van començar a fer música molt abans de saber res de tot això. I, enlloc de parlar de freqüències (vibracions per segon) van buscar maneres d’escriure i parlar del to d’un so musical. A Occident, es van acabar fent servir els noms de les notes que avui en dia coneixem: Do, Re, Mi, Fa, Sol, La Si, que en el sistema anglès duen les lletres C, D, E, F, G, A, B. El La, en particular és el nom que donem a un so musical que vibra 440 vegades per segon.

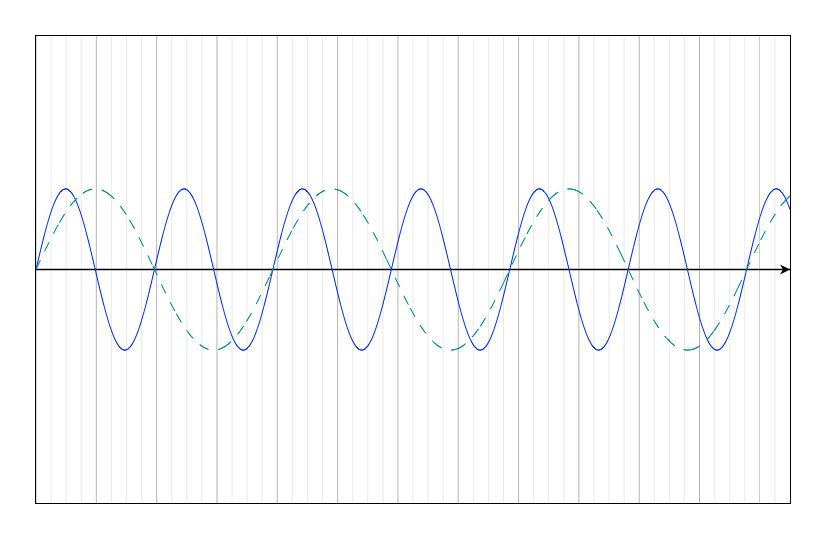
Però amb només 7 noms de notes com podem referir-nos a totes les freqüències entre 20 Hz i 20.000 Hz? Hi ha un fernòmen que explica que puguem fer-ho. A mesura que anem augmentant el to (fent més aguda) una determinada nota, hi ha un moment que notem una semblança amb la nota de partida, com si estiguessim escoltant una versió més aguda de la mateixa nota. Físicament s’explica perquè les ones de la nota més aguda i la més greu estan “sincronitzades”, de tal manera que cada ona de la nota greu en correspon a dues de l’aguda:

!le.jpg)

Per tant, si agafem una nota qualsevol i en doblem la freqüència obtenim un to al que donem el mateix nom de nota. Així, si el so musical de 440 Hz l’anomenem La, el de 880, també. I, les notes que coneixem es van repetint cada cop que doblem la freqüència del so:

La (440 Hz), Si, Do, Re, Mi, Fa, Sol, La (880 Hz), Si, Do, Re, Mi, Fa, Sol, La (1.760 Hz)…

Si mirem les tecles d’un piano veurem que, efectivament, hi ha un patró que es repeteix cada 7 tecles blanques:

Foto: Photo of Piano Keys de Karyme França a Pexels

Com que comptant de La a La hi escribim 8 notes (i per despistar als novells que tenim una mentalitat matemàtica), de les notes que hi ha entre una nota i la següent del mateix nom en diuen octava. El La de 440 Hz diem que és de la quarta octava i, al sistema internacional, l’indiquem com La4 ³.

Les notes blanques del piano corresponen, doncs, amb els set noms de nota que es van repetint a cada octava:

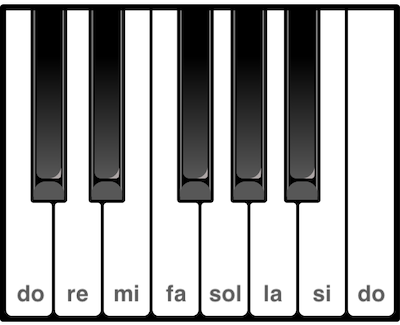Clipart: A piano keyboard octave de Domini públic

Podríem pensar que les freqüències entre els dos La de l’exemple es reparteixen de forma equitativa⁴ entre els 6 espais entre notes… però no és així. De fet, al piano, entre una nota i la segúent del mateix nom (entre el Do i el Do de la figura de dalt, per exemple), hi ha 12 tecles, no pas només set: les set blanques i cinc tecles negres.

En música es diu que entre cada dues tecles del piano hi ha un semitò de distància. Entre dues notes del mateix nom hi ha, doncs, 12 semitons de distància. I el nom de les notes es reparteix d’una forma particular:

entre el…	i el …	hi ha…
Do	Re	2 semitons
Re	Mi	2 semitons
Mi	Fa	1 semitò
Fa	Sol	2 semitons
Sol	La	2 semitons
La	Si	2 semitons
Si	Do	1 semitò

I com anomenem les 5 notes que no han rebut cap dels noms que coneixem? Vegem-ho a la propera entrada.

---